Relations
CSE 16: Applied Discrete Mathematics
Instructor: Owen Arden
Winter 2023
Binary relations
- Binary relation
- A binary relation expresses a property on elements in two sets. The relation R on sets \(A\) and \(B\) is a subset of \(A \times B\). For \(a \in A\) and \(b \in B\), we write \(aRb\) when \((a, b) \in R\).
Example: Suppose \(C\) is the set of colleges on campus and \(S\) is the set of students. The relation \(A \subseteq S \times C\) indicates whether a student \(s \in S\) is affiliated with a college \(c \in C\).
- Is this statement true \(\forall s.\forall c. (s \in S \wedge c \in C) \to
sAc\) ?
- What about graduate students?
- Is this statement true \(\forall s \in S.\forall c \in C. sAc \to \forall c' \in C. c' \neq c \to \neg sAc'\) ?
Properties of relations
It is often useful to define universal properties of the elements in a relation.
- Reflexivity
- A binary relation \(R\) on set \(A\) (\(R \subseteq A \times A\)) is reflexive iff \(\forall x \in A. xRx\).
- Examples?
- Anti-reflexivity
- A binary relation \(R\) on set \(A\) (\(R \subseteq A \times A\)) is anti-reflexive iff \(\forall x \in A. \neg xRx\).
- Examples?
Properties of relations
- Symmetricity
- A binary relation \(R\) on set \(A\) is symmetric iff \(\forall x,y \in A. xRy \leftrightarrow yRx\).
Examples?
Is “relative of” symmetric?
Is \(<\) symmetric?
Is \(=\) symmetric?
Is \(\leq\) symmetric?
Properties of relations
- Anti-symmetricity
- A binary relation \(R\) on set \(A\) is anti-symmetric iff \(\forall x,y \in A. x \neq y \to \neg (xRy \wedge yRx)\).
Examples?
Can any relation be both symmetric and anti-symmetric?
Can any relation be neither symmetric nor anti-symmetric?
Is “parent of” anti-symmetric?
Is \(=\) anti-symmetric?
Is \(<\) anti-symmetric?
Is \(\leq\) anti-symmetric?
Properties of relations
- Transitivity
- A binary relation \(R\) on set \(A\) is transitive iff \(\forall x,y,z \in A. (xRy /\ yRz) \to xRz\).
- Examples?
- Is \(\to\) a transitive relation?
- Is \(\subset\) a transitive relation?
- Is \(\in\) a
transitive relation?
- \(a \in A \wedge A \in B\) does not (necessarily) imply \(a \in B\)
- but it could, von Neumann ordinals: \(\emptyset, \{ \emptyset \}, \{ \emptyset, \{ \emptyset \} \}\).
Properties of relations
Other questions:
- Are all binary relations functions?
- No, there could be distinct elements \(a,b,c\) of \(A\) such that \(aRb\) and \(aRc\).
- Are all functions binary relations?
- Yes, a function \(f\) with domain \(A\) and codomain \(B\) can be represented as a subset \(S\) of \(A \times B\) such that \((a,b) \in S\) iff \(f(a) = b\).
Relations as directed graphs
- Directed graph
- A directed graph or digraph is a pair of sets \((V,E)\) where \(V\) represents the set of vertices in the graph, and \(E \subseteq V \times V\) represents the edges between them.
Example: \[\begin{align} V &= \{w,x,y,z\} \\ E &= \{(w,x), (x,y), (w,y), (y,z) \} \end{align}\]
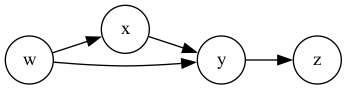
Directed graphs can represent binary relations on a set \(V\)!
Graph terms and properties
- in-degree
- The in-degree of a vertex is the number of edges pointing to it.
- out-degree
- The out-degree of a vertex is the number of edges pointing out of it.
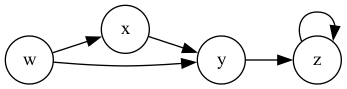
Graph terms and properties
- walk
- A walk between vertices \(v_1\) and \(v_2\) is a connected sequence of vertices and edges beginning at \(v_1\) and ending at \(v_2\). The length of a walk is the number of edges in the sequence.
- open and closed walks
-
An open walk is a walk between \(v_1\) and \(v_2\) where \(v_1
\neq v_2\).
A closed walk is a walk between \(v_1\) and \(v_2\) where \(v_1 = v_2\).
- trail
- A trail is a walk with no repeated edges.
- path
- A path is a walk with no repeated vertices.
- circuit
- A circuit is a closed trail.
- cycle
- A cycle is a circuit of length 1 or more where no vertex is repeated except for the first and last.
Graph terms and properties
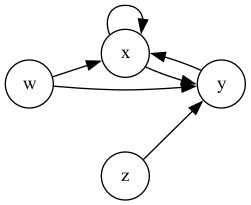
Graph composition
- composition
- The composition of relations \(R\) and \(S\) on \(A\) is another relation written \(S \circ R\). \((a,c)\in S \circ R\) iff there exists a \(b \in A\) such that \((a,b) \in R\) and \((b,c) \in S\).
- graph powers
- For a graph \(G = (V,E)\), the \(k^{th}\) power of \(G\),written \(G^{k}\), is the composition of the edge relation \(E\) \(k\) times, written \(E^{k}\) where \(E^{1}=E\) and \(E^{k} = E \circ E^{k-1}\) (for \(k \geq 2\)).
Graph power theorem: Let \(G\) be a directed graph. Let \(u\) and \(v\) be any two vertices in \(G\) There is an edge from \(u\) to \(v\) in \(G^{k}\) iff there is a walk of length \(k\) from \(u\) to \(v\) in \(G\).
Transitive closure
- transitive closure
- The transitive closure of R is the smallest relation \(R^{+}\) such that \(R^{+}\) is transitve and \(R \subseteq R^{+}\).